La crise financière que nous traversons actuellement favorise une pratique vieille comme le monde : la fraude comptable et financière. Que ce soit pour dissimuler un détournement de fonds ou maquiller des états financiers pour cacher la réalité de la situation du patrimoine d’une entreprise, le fraudeur use d’artifices pour repousser la découverte de son forfait.
Bien que les missions de l’expert-comptable et du commissaire aux comptes n’aient pas pour objet la recherche de la fraude, ils doivent faire preuve de vigilance et faire oeuvre d’esprit critique.
Fréquence d’apparition de chaque chiffre significatif selon la Loi de Benford
Le commissaire aux comptes et l’expert-comptable (missions de grande révision) disposent d’outils simples d’aide à la détection de la fraude. J’en avais exposé deux exemples dans mon mémoire d’expertise-comptable : un tableau de bord comptable synthétique (sous la forme d’un tableau croisé dynamique) et l’utilisation de la loi de Benford (il s’agit d’une loi mathématique et non pas d’une énième invention réglementaire chère à notre législateur). Ces deux outils pratiques, aisés à mettre en oeuvre sous EXCEL, sont une bonne introduction à l’analyse de données. Ces outils ne sont pas infaillibles et ne permettent pas de détecter toutes les formes de fraudes, toutefois ils forment une panoplie d’indicateurs d’alerte qui orientent le professionnel du chiffre dans ses travaux tout en assurant son devoir de vigilance prévu par ses normes professionnelles.
C’est ce deuxième outil, la Loi de Benford, que je vais exposer ci-après.
Découverte dès 1881 par l’astronme américain Simon NEWCOMB, redécouverte vers 1938 par Frank BENFORD et démontrée en 1996 par Theodore P. HILL, la loi de Benford (ou loi des nombres anormaux) indique que la fréquence d’apparition du premier chiffre significatif d’un nombre répond à une distribution prédéterminée. Le premier chiffre significatif d’un nombre est le chiffre le plus à gauche différent de zéro. Par exemple : le premier chiffre significatif de 1325,72 est 1, le premier de 0,753 est 7.
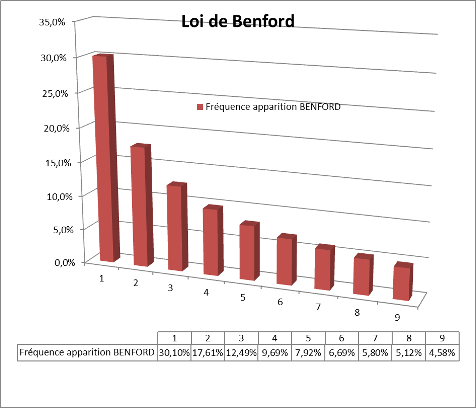
Le graphique (cf plus haut) montre que la fréquence d’apparition du chiffre 1 est de 30,10 %, celui du 2 de 17,61%… Cette fréquence a été observée, aussi étonnant que cela puisse paraître, sur de nombreuses listes : longueur de fleuves, populations de pays… Les données comptables n’échappent pas à cette règle. Le fisc américain l’utilise pour déceler les cas de fraude fiscale. En effet, les manipulations comptables du fraudeur seront susceptibles de ne pas respecter la distribution théorisée par la loi de Benford.
Application de la Loi de Benford sur un échantillon d’écritures comptables
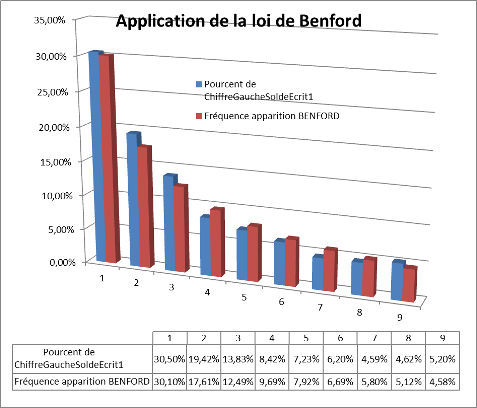
Le décompte des chiffres significatifs observés dans l’échantillon des données auditées (ici des écritures comptables) est rapproché des fréquences théoriques calculées à partir de la loi de Benford. Dans le graphique précédent, 30,50% des données du grand livre audité (fréquence observée) commencent par le chiffre 1 (pour mémoire, la loi de Benford prévoit 30,10%, fréquence théorique).
L’écart entre les fréquences observées et les fréquences théoriques est soumis au test du KHI DEUX (X²). Le KHI² se calcule ainsi :
(fréquence observée – fréquence théorique)² / fréquence théorique
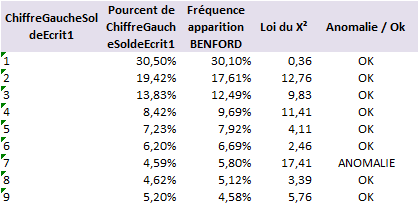
Tout résultat du test supérieur à 15,5 révèle une anomalie avec au plus 5 % de risque de se tromper. Pour reprendre notre exemple appliqué à un grand livre, nous obtenons ceci :
Résultat du Test du KHI²
Les nombres commençant par le chiffre 7 sont sous-représentés dans le grand livre. Cette observation génère un Khi² de 17,41 et potentiellement une anomalie (car Khi² supérieur à 15,5). Reste à trouver une explication…
Si la fréquence d’apparition des chiffres significatifs d’une liste donnée diffère sensiblement de celle de la loi de Benford, on peut supposer que nous sommes en présence d’anomalies ou, dans le cadre de données comptables ou financières, de fraudes.
L’absence d’anomalie révélée par la loi de Benford ne signifie pas nécessairement qu’il n’y a aucune fraude. Il s’agit simplement d’un indicateur.
L’application de la loi de Benford connaît tout de même une exception : les nombres ne doivent pas être contraints ou biaisés par un paramètre qui entraînerait une surreprésentation d’un chiffre donné. Imaginons le cas d’une billeterie qui vend des entrées au prix unique de 6 €. La fréquence d’apparition du chiffre 6 attirera l’attention sans qu’il y ait pour autant d’anomalie réelle.
Une fois les conclusions tirées, il suffit d’extrapoler le résultat de l’échantillon sur la population toute entière avec un niveau de confiance de 95 % et le cas échéant rechercher les éléments probants étayant la fraude (ou l’anomalie).
Le lecteur pourra utilement se référer à l’article intitulé « Loi de Benford » consultable à cette adresse URL : http://fr.wikipedia.org/wiki/Loi_de_Benford notamment pour en savoir plus sur l’histoire de la découverte de cette loi et comprendre la règle mathématique prescrivant la fréquence d’apparition.
Mise à jour du 7/01/2014 :
Plusieurs lecteurs m’ont fait observé qu’ils ne parvenaient pas à recalculer le Khi² à partir de l’exemple du présent article.
En fait, le Khi² est obtenu à partir des fréquences absolues. Or, le tableau publié plus haut ne reprend que les valeurs relatives, induisant de fait le lecteur attentif en erreur.
Le tableau ci-après reprend l’ensemble des données chiffrées nécessaires au calcul du Khi² :
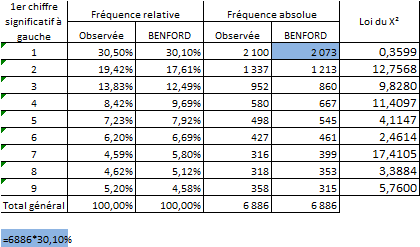Exemple : (2100-2073)^2/2073=0,3599
Je vous remercie de vos observations. Au passage, je constate que la loi de Benford intrigue et intéresse les lecteurs de ce blog. N’hésitez pas à me faire part de votre expérience avec la loi de Benford.
En savoir plus sur le sujet :
Découvrir tous les articles en rapport avec la fraude.
Un exemple d’application d’analyse de données mettant en oeuvre la loi de Benford.
Derniers articles parBenoît RIVIERE (voir tous)
- Excel : collecter des données juridiques sur les entreprises avec l’API SIRENE – 1ère partie : base SIREN (entreprises) - lundi 15 avril 2024
- Obtenir les données financières de sociétés au format Excel - mardi 2 avril 2024
- Robotic Process Automation (RPA) et Python : piloter des applications web - dimanche 24 mars 2024
- Initiation à la programmation en Basic : nouveau compilateur FreeBASIC - lundi 18 mars 2024
- Retrogaming : (re)jouer aux jeux vidéo d’antan - lundi 11 mars 2024
toujours intéressant d’avoir des tests complémentaires
auriez vous une formule excel qui permettrait de d’indiquer le chiffre siginficatif
merci pour votre blog toujours utile
Bonsoir,
Pour récupérer le premier chiffre significatif : =GAUCHE(ABS(A1*100);1)
Bonne continuation,
Cordialement,
Benoît RIVIERE
Bonjour et merci pour cet article très intéressant.
Je ne parviens pas à calculer le X² en utilisant la formule que vous indiquez (mes résultats sont tout à fait différents). Pouvez-vous préciser votre méthode ?
Merci,
Bonsoir,
Merci de votre commentaire et de votre intérêt pour mon article.
D’autres lecteurs m’ont fait part des mêmes difficultés dans le calcul du Khi². J’ai apporté des informations complémentaires à la fin de l’article qui devraient lever toutes les interrogations.
N’hésitez pas à me communiquer vos réactions ou suggestions, je répondrai bien volontiers.
Cordialement,
Benoît RIVIERE
Bonjour
Je suis Stagiaire Expert Comptable et je souhaiterais vous remercier pour vos articles. Ils ont le mérite d’être clair et d’aller à l’essentiel. J’ai le même gout pour l’organisation et l’analyse de données (même si je n’ai pas connu l’informatique des années 1980 ! ). D’une façon générale, à votre avis, est il possible de construire des programmes VBA ou Excel pour l’audit qui soient utilisables pour les utilisateurs neophytes ?
Bonjour,
Bien sûr. Excel est totalement paramétrable. Avec le VBA ou sans d’ailleurs. Il est ainsi possible de rajouter des menus ou de passer par des fenêtres d’options et ainsi de construire facilement une interface qui permet un utilisateur débutant de se servir d’Excel sans peine (pour des utilisations très précises comme l’analyse de données ou pour formaliser un dossier de commissariat aux comptes). Si vous consultez mes “Réalisations personnelles”, vous verrez que c’est que j’ai entrepris dans différents projets informatiques que j’ai menés.
Bon courage pour votre stage.
Cordialement,
Benoît RIVIERE
Bonjour,
Le calcul du X² ne devrait-il pas s’appliquer sur la somme des résidus et non pas ligne à ligne ? Ainsi, la somme des résidus ne devrait pas dépasser 15.5 à 8 degrés de liberté. Les chiffres qui poseraient donc problème seraient: 2,4,7 à première vue et non le 7 exclusivement.
Cordialement
Bonjour,
Votre question dépasse mes compétences. J’ai mis en application ce que j’ai compris de mes recherches sur internet. Si vous avez des compléments d’information sur le sujet, n’hésitez pas à revenir vers moi, cela m’intéresse.
Bien cordialement,
Benoît RIVIERE
Pingback: Yotta Conseil » Traitement de fichiers des écritures comptables FEC
Bonjour,
J’approuve la remarque faîte dans le dernier commentaire. C’est la somme de la colonne “Loi du χ²” qui doit être inférieure à 15.5 pour pouvoir affirmer que l’échantillon suit bien la loi de Benford, au risque de se tromper de 5%.
L’échantillon serait donc invalidé dans son ensemble (avec un risque d’erreur de 5%)
Cordialement
Bonjour et merci pour votre article.
j’ai une question concernant la phrase “Les nombres commençant par le chiffre 7 sont sous-représentés dans le grand livre “, quelles seraient les explications (ou hypothèses) d’une sous-représentation de nombre?
Je fais appel à votre expérience.
En vous remerciant par avance.
Nicolas
Bonjour,
Il n’y a pas de réponse unique. La recherche de la source de la discordance n’est généralement pas simple. A titre personnel, je n’utilise pas au quotidien la Loi de Benford parce que la recherche de l’explication des discordances pose plus de questions que de réponses…
Cordialement,
Benoît RIVIERE
Ok merci pour votre retour.
Bonne continuation.
Bien cordialement,
Nicolas